¿Cómo calcular la medida de altura de las pirámides por medio del teorema de Tales de Mileto?

Dos triángulos son semejantes si tienen los ángulos correspondientes iguales y sus lados son proporcionales entre sí.



"Si en un triángulo se traza una línea paralela a cualquiera de sus lados, se obtiene un triángulo que es semejante al triángulo dado."









Tales descubrió el teorema mientras investigaba la condición de paralelismo entre dos rectas. De hecho, el primer teorema de Tales puede enunciarse como que la igualdad de los cocientes de los lados de dos triángulos no es condición suficiente de paralelismo.




Del establecimiento de la existencia de una relación de semejanza entre ambos triángulos se deduce la necesaria proporcionalidad entre sus lados. Ello significa que la razón entre la longitud de dos de ellos en un triángulo se mantiene constante en el otro.




A modo de corolario que el cociente entre los lados A y B del triángulo pequeño es el mismo que el cociente entre los lados D y C en el triángulo grande. Esto es, que como por el teorema de Tales ambos triángulos son semejantes, se cumple que:









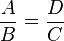
El primer teorema de Tales se deduce además lo siguiente: (Si las rectas A, B, C son paralelas y cortan a otras dos rectas R y S, entonces los segmentos que determinan en ellas son proporcionales.

¿Cómo midió Tales de Mileto la altura de la Pirámide de Keops?

Cuenta la historia...

Que un sacerdote egipcio le preguntó a Tales de Mileto a cerca de la altura de la Pirámide de Keops, cuando ya las pirámides rondaban los 2.000 años de edad, y éste respondió con un método muy ingenioso para medir dicha altura.



Tales ante la pregunta, reflexiona y a continuación contesta que no se conforma con calcularla a ojo, sino que la medirá sin ayuda de ningún instrumento. Se echa sobre la arena y determina la longitud de su propio cuerpo.



Los sacerdotes le preguntan qué es lo que está pensando, y Tales les explica: ‘Me pondré simplemente en un extremo de esta línea, que mide la longitud de mi cuerpo, y esperaré hasta que mi sombra sea igual de larga. En ese instante , la sombra de la pirámide de vuestro Khufu también ha de medir tantos pasos como la altura de la pirámide.’

El sacerdote, desorientado por la extrema sencillez de la solución, se pregunta si acaso no hay algún error, algún sofisma, Tales añade: ‘Pero si queréis que os mida esa altura, a cualquier hora, clavaré en la arena mi bastón.”

El método que utilizó Tales de Mileto para calcular la altura de la Pirámide de Keops es lo que conocemos como Teorema de Tales.

La sombra es la región donde no dan los rayos del sol. Se supone que los rayos que inciden en la pirámide y en el bastón son paralelos (consecuencia de la gran distancia que separa al Sol de la Tierra) y el bastón está clavado perpendicularmente al suelo.


De esta forma, los ángulos de los dos triángulos que observamos en la figura son iguales entre sí y, por tanto, dichos triángulos son semejantes. En dos triángulos semejantes, se cumple que sus lados homólogos son proporcionales.
En nuestro caso, se cumple que:

Referencias:

Amadeo Artacho. (2014). La Pirámide de Keops. 03/03/2016, de matematicascercanas Sitio web: http://matematicascercanas.com/2014/04/06/la-piramide-de-keops/#