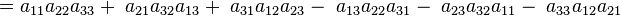Espacio Tecnológico
domingo, 22 de noviembre de 2015
miércoles, 18 de noviembre de 2015
Matriz
¿Cuál es la relación de las matrices y los sistemas de ecuaciones con tres incógnitas?
Cuando existe un sistema de tres ecuaciones es asociado con dos matrices, A matriz de coeficientes y A* matriz amplia ( a la primera matriz se le agrega solamente la columna de los términos independientes).
"
Para resolver hay varios métodos:
- Método de Gauss: Tomamos las matriz ampliada asociada al sistema y hacemos las trasformaciones de filas necesarias para hacer la matriz de coeficientes triangular, a partir de ahí deducimos los valores de las variables.
- Matríz inversa: Si expresamos el sistema en forma matricial AX=B y A es inversible entonces
 donde X es la matriz de variables A la de coeficientes y B la de términos independientes. Condición necesaria es que exista la inversa de A
donde X es la matriz de variables A la de coeficientes y B la de términos independientes. Condición necesaria es que exista la inversa de A
- Regla de Cramer:El valor de la variable i-ésima se obtiene del cociente C/D, donde C es el determinante de la matriz de coeficientes donde se cambia la columna i-ésima por la columna de términos independientes y D es el determinante de la matriz de coeficientes.
- Método de Gauss: Tomamos las matriz ampliada asociada al sistema y hacemos las trasformaciones de filas necesarias para hacer la matriz de coeficientes triangular, a partir de ahí deducimos los valores de las variables.
- Matríz inversa: Si expresamos el sistema en forma matricial AX=B y A es inversible entonces
 donde X es la matriz de variables A la de coeficientes y B la de términos independientes. Condición necesaria es que exista la inversa de A
donde X es la matriz de variables A la de coeficientes y B la de términos independientes. Condición necesaria es que exista la inversa de A
- Regla de Cramer:El valor de la variable i-ésima se obtiene del cociente C/D, donde C es el determinante de la matriz de coeficientes donde se cambia la columna i-ésima por la columna de términos independientes y D es el determinante de la matriz de coeficientes.".-ematematicas.net
La relación de estas operaciones matemáticas es que para poder resolver un sistema de tres ecuaciones son automáticamente asociadas con las dos matrices que está conlleva, (A y A*) aunque estas matrices de igual manera son divididas en diferentes, tales como, cuadradas, de fila, cuadradas, etc.
miércoles, 4 de noviembre de 2015
Regla de Sarrus
La regla de Sarrus es utilizada para poder calcular un determinante de forma 3x3 y recibe ese nombre del matemático francés Pierre Frédéric Sarrus.

Datos importantes:
Para poder calcular utilizaremos la siguiente matriz:

Habrá que repetir las dos primeras columnas de la matriz a la derecha de la misma de manera que queden cinco columnas en fila. Después se sumarán los productos de las diagonales descendentes (en línea continua) y sustraer los productos de las diagonales ascendentes (en trazos).
Datos importantes:
- El valor de un determinante es igual a la suma de productos de los elementos de una línea por sus adjuntos correspondientes.
- Si en un determinante se cambian entre sí dos filas (o dos columnas) su determinante cambia de signo.
- El determinante de un producto es igual al producto de los determinantes.
domingo, 18 de octubre de 2015
Resolver Ecuaciones en Hojas de Cálculo
USO DE UNA HOJA DE CÁLCULO PARA RESOLVER ECUACIONES
La capacidad para crear gráficas de las Hojas de Cálculo, es una herramienta que puede comprometer conceptualmente a los estudiantes y ayudarles a ver las ecuaciones y sus soluciones de nuevas maneras. Los ejemplos que se usan en este artículo se hicieron utilizando la Hoja de Cálculo de “Claris Works” pero el proceso puede adaptarse fácilmente a cualquier programa de Hoja de Cálculo.
Ejemplo 2:
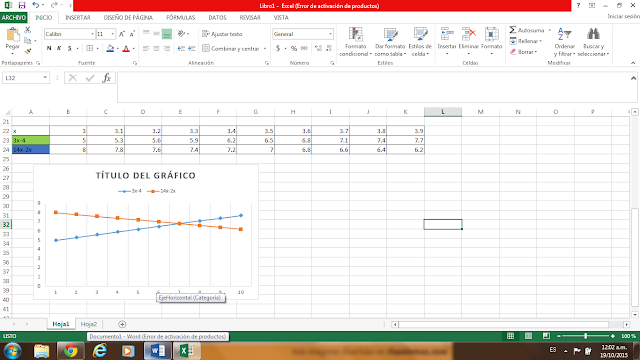
información citada desde :
Margaret L. Niess. (2003). CÓMO UTILIZAR LAS HOJAS DE CÁLCULO PARA RESOLVER ECUACIONES. 19/10/15, de Eduteka Sitio web: http://www.eduteka.org/HojaCalculo1.php
La capacidad para crear gráficas de las Hojas de Cálculo, es una herramienta que puede comprometer conceptualmente a los estudiantes y ayudarles a ver las ecuaciones y sus soluciones de nuevas maneras. Los ejemplos que se usan en este artículo se hicieron utilizando la Hoja de Cálculo de “Claris Works” pero el proceso puede adaptarse fácilmente a cualquier programa de Hoja de Cálculo.
Ejemplo 1:
Ejemplo 2:

información citada desde :
Margaret L. Niess. (2003). CÓMO UTILIZAR LAS HOJAS DE CÁLCULO PARA RESOLVER ECUACIONES. 19/10/15, de Eduteka Sitio web: http://www.eduteka.org/HojaCalculo1.php
Aplicación de Binomios al Cuadrado en el Área de un Cuadrado
Binomios al Cuadrado
Nosotros buscamos como aplicar el binomio al cuadrado en esta fórmula, por lo que sustituiremos, los valores de L por binomios.
A continuación se pondrá un ejemplo del calculo del área de un cuadrado aplicando un binomio al cuadrado:
Analhayet quiere saber el área de un cuadrado de un ajedrez gigante que hicieron los alumnos de primer semestre para la materia de Matemáticas 1, conoce la medida de un lado, que es x+9, y ella sabe que para calcular el área de un cuadrado la fórmula es: L*L, así que opta por despejar la fórmula de la siguiente manera:
A= L*L
L= x+9
A= (x+9)(x+9)
A= (x+9)2
A= a2+2ab+b2
A=x2+2(x)(9)+(9)2
A= x2+18x+81
Así que el resultado de la operación será x2+18x+81
Aplicación del Producto de Polinomios
Productos de Polinomios
Para multiplicar dos polinomios multiplicamos cada monomio del primer polinomio por cada polinomio del segundo. Luego sumamos aquellos monomios con la misma parte literal.
Ejemplo:
Mi papá mandó a construir una caja madera para almacenar herramientas, y para construirla, el carpintero, pidió ciertos criterios que mi papá quisiera para construirla, los cuales fueron, que el volumen final de la caja, expresado en una ecuación, fuera de 5x2-100x+500, por lo que el carpitero al no entender muy bien el criterio, le pidió que le diera las medidas exactas, a lo que mi papá le ayudo brindandole la operación de este producto, que era así:
V=Ab*h

Ab= (x-10)
h= (x-10)5
(x-10)(x-10)= x2-10x-10x+100=x2-20x+100
(x2-20x+100)(5)=
y de esta manera el carpintero pudo hacer una hermosa caja.
jueves, 24 de septiembre de 2015
La Historia de Gauss
Anecdota de niño de Gauss
Espacio Tecnológico
Espacio Tecnológico
¿ Cuál es el estado más poblado de nuestro país?
El Estado de México con 15,175,862
¿ Cuál es el estado más poblado de nuestro país?
El Estado de México con 15,175,862
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
¿Cuál es la tasa de crecimiento en México durante los últimos 5 años?
De 1,21%
Fuente bibliográfica:
http://cuentame.inegi.org.mx/poblacion/mujeresyhombres.aspx?tema=P
http://www.indexmundi.com/es/mexico/tasa_de_crecimiento.html
miércoles, 23 de septiembre de 2015
números enteros
Espacio Tecnológico
Para controlar sus gasto Abigail utiliza un signo positivo si recibe dinero y un signo negativo si realiza un gasto. Lleva su registro quincenal.
Ayuda a Abigail creándole una hoja de Excel para poder administrar sus gastos.
Para controlar sus gasto Abigail utiliza un signo positivo si recibe dinero y un signo negativo si realiza un gasto. Lleva su registro quincenal.
Ayuda a Abigail creándole una hoja de Excel para poder administrar sus gastos.
¿Quién fue Fibonacci?
espacio tecnológico
Leonardo de Pisa, Leonardo Pisano o Leonardo Bigollo (c. 1170 - 1250), también llamado Fibonacci, fue un matemático italiano, famoso por haber difundido en Europa el sistema de numeración indo-arábigo actualmente utilizado, el que emplea notación posicional (de base 10, o decimal) y un dígito de valor nulo: el cero; y por idear la sucesión de Fibonacci.
La sucesión comienza con los números 1 y 1, y a partir de estos, «cada término es la suma de los dos anteriores», es la relación de recurrencia que la define.
la regla es xn = xn-1 + xn-2
donde:
Leonardo de Pisa, Leonardo Pisano o Leonardo Bigollo (c. 1170 - 1250), también llamado Fibonacci, fue un matemático italiano, famoso por haber difundido en Europa el sistema de numeración indo-arábigo actualmente utilizado, el que emplea notación posicional (de base 10, o decimal) y un dígito de valor nulo: el cero; y por idear la sucesión de Fibonacci.
La sucesión comienza con los números 1 y 1, y a partir de estos, «cada término es la suma de los dos anteriores», es la relación de recurrencia que la define.
La regla
La sucesión de Fibonacci se puede escribir como una "regla" (lee sucesiones y series):la regla es xn = xn-1 + xn-2
donde:
- xn es el término en posición "n"
- xn-1 es el término anterior (n-1)
- xn-2 es el anterior a ese (n-2)
x6 = x6-1 + x6-2 = x5 + x4 = 5 + 3 = 8
MÁXIMO COMÚN DIVISOR
Máximo común divisor
Mayor número o polinomio que divide exactamente dos o más números o polinomios.
El máximo común divisor (MCD) de dos o más número natural o enteros (no números con decimales) es el número más grande que les divide.Para número más grandes es más fácil hacer una descomposición en factores primos. Esta descomposición la empezamos siempre con el número más pequeño divisible del número que analizamos.
10 5
0 2
10 6
4 1
4 1
6 No sería divisor de 10 porque el resto da 4 y tiene que ser 0.
Una vez sabido que los divisores de 10 y de 20 son:
Divisor de 20: 1, 2, 4, 5, 10 y 20.
Divisor de 10: 1, 2, 5 y 10.
Vamos a ver cuáles son los números que coinciden que son:
Divisor de 20: 1, 2, 4, 5, 10 y 20.
Divisor de 10: 1, 2, 5 y 10.
Divisores de 10 y 20 son: 1, 2, 5 y 10.
El máximo común divisor sería el 10 porque es el número más grande que, a su vez, es divisor de ambos número (10 y 20).
jueves, 10 de septiembre de 2015
Porcentaje de Habitantes
Porcentaje de Población
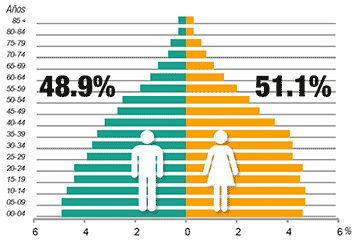
¿Qué porcentaje de hombres y mujeres hay en tu localidad?
mujeres:50.8%
hombres:49.2%
Total: 2 238 603 habitantes (100%)
¿Qué porcentaje de habitantes hay con respecto a todo el país?
112 336 538 Millones de Habitantes en México.
1.99% Número de Habitantes en Tabasco con Respecto a México.
La Criba de Eratóstenes
¿Cómo se forma la Criba de Eratóstenes?
Se forma una tabla con todos los números naturales comprendidos entre 2 y n, y se van tachando los números que no son primos de la siguiente manera: Comenzando por el 2, se tachan todos sus múltiplos; comenzando de nuevo, cuando se encuentra un número entero que no ha sido tachado, ese número es declarado primo, y se procede a tachar todos sus múltiplos, así sucesivamente. El proceso termina cuando el cuadrado del mayor número confirmado como primo es mayor que n.
Eratóstenes
Eratóstenes
Eratóstenes fue
un matemático,astrónomo y geógrafo griego,
de origen cirenaico, una de las figuras más eminentes del gran
siglo de la ciencia griega: el de Euclides, Arquímedes y
Apolonio.
Fue célebre en matemáticas por la criba que lleva su nombre, utilizada para
hallar los números primos, y por su mesolabio, instrumento de cálculo usado
para resolver la media proporcional.


Es particularmente recordado por
haber establecido por primera vez la longitud de la circunferencia de la Tierra
(252.000 estadios, equivalentes a 40.000 kilómetros) con un error de sólo 90
kilómetros respecto a las estimaciones actuales.
Calculó la oblicuidad de la eclíptica por medio de la observación de las
diferencias existentes entre las altitudes del Sol durante los solsticios de
verano e invierno, y además elaboró el primer mapa del mundo basado en
meridianos de longitud y paralelos de latitud.
http://www.biografiasyvidas.com/biografia/e/eratostenes.htm
Eratóstenes
Suscribirse a:
Comentarios (Atom)