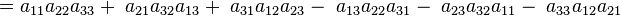Matemáticas II: noviembre 2015

miércoles, 18 de noviembre de 2015

Matriz

¿Cuál es la relación de las matrices y los sistemas de ecuaciones con tres incógnitas?

Cuando existe un sistema de tres ecuaciones es asociado con dos matrices, A matriz de coeficientes y A* matriz amplia ( a la primera matriz se le agrega solamente la columna de los términos independientes).

"
Para resolver hay varios métodos:

Método de Gauss: Tomamos las matriz ampliada asociada al sistema y hacemos las trasformaciones de filas necesarias para hacer la matriz de coeficientes triangular, a partir de ahí deducimos los valores de las variables.

Matríz inversa: Si expresamos el sistema en forma matricial AX=B y A es inversible entonces donde X es la matriz de variables A la de coeficientes y B la de términos independientes. Condición necesaria es que exista la inversa de A

Regla de Cramer:El valor de la variable i-ésima se obtiene del cociente C/D, donde C es el determinante de la matriz de coeficientes donde se cambia la columna i-ésima por la columna de términos independientes y D es el determinante de la matriz de coeficientes.

Método de Gauss: Tomamos las matriz ampliada asociada al sistema y hacemos las trasformaciones de filas necesarias para hacer la matriz de coeficientes triangular, a partir de ahí deducimos los valores de las variables.

Matríz inversa: Si expresamos el sistema en forma matricial AX=B y A es inversible entonces donde X es la matriz de variables A la de coeficientes y B la de términos independientes. Condición necesaria es que exista la inversa de A

Regla de Cramer:El valor de la variable i-ésima se obtiene del cociente C/D, donde C es el determinante de la matriz de coeficientes donde se cambia la columna i-ésima por la columna de términos independientes y D es el determinante de la matriz de coeficientes.".-ematematicas.net

La relación de estas operaciones matemáticas es que para poder resolver un sistema de tres ecuaciones son automáticamente asociadas con las dos matrices que está conlleva, (A y A*) aunque estas matrices de igual manera son divididas en diferentes, tales como, cuadradas, de fila, cuadradas, etc.

miércoles, 4 de noviembre de 2015

Regla de Sarrus

La regla de Sarrus es utilizada para poder calcular un determinante de forma 3x3 y recibe ese nombre del matemático francés Pierre Frédéric Sarrus.

Para poder calcular utilizaremos la siguiente matriz:

M = \begin{pmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{pmatrix}

Habrá que repetir las dos primeras columnas de la matriz a la derecha de la misma de manera que queden cinco columnas en fila. Después se sumarán los productos de las diagonales descendentes (en línea continua) y sustraer los productos de las diagonales ascendentes (en trazos).

$\det \begin{pmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{pmatrix} = \begin{vmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{vmatrix} =$

$= a_{11} a_{22} a_{33} + \; a_{21} a_{32} a_{13} + \; a_{31} a_{12} a_{23} - \; a_{13} a_{22} a_{31} - \; a_{23} a_{32} a_{11} - \; a_{33} a_{12} a_{21}$